Cara Membuat Diagram Kartesius dan Contoh Soal

Materi Koordinat Cartesius kelas 8 Lengkap☑️ Cara membuat diagram kartesius beserta gambar dan contoh soal + pembahasan☑️

Topik mengenai diagram Kartesius sudah tidak asing lagi, setidaknya bagi mereka yang pernah mengenyam pendidikan di bangku SMP. Biasanya, diagram ini merujuk pada visualisasi sebuah himpunan yang diwakili oleh sumbu X dan Y.

Namun, tahukah Anda? Lebih dari sekadar pelajaran sewaktu sekolah, pemanfaatan diagram Kartesius ternyata umum ditemukan dalam kehidupan sehari-hari, khususnya di kalangan akademisi.

Pengertian Diagram Kartesius

Istilah Kartesius(cartesius) berasal dari nama Ilmuwan Matematika asal Perancis khususnya pada cabang ilmu aljabar dan geometri. Cartesius merupakan serapan dari asal kata Descartes.

Dari teori Descartes yang ditulis dalam sebuah buku Discourse on the method dijabarkan bahwa kartesius merupakan sebuah metode untuk mengvisualisasikan posisi sebuah titik menggunakan dua sumbu tegak lurus. Dari teori inilah muncul istilah Koordinat kartesius.

Koordonat karteius merupakan metode yang menyatakan posisi titik dalam bidang menggunakan pasangan bilangan absis yaitu koordinat X dan ordinat Y dari titik tersebut. Lalu apa itu diagram kartesius ?

Diagram Kartesius (Cartesius) adalah jenis diagram yang terdiri dari sistem koordinat sumbu X dan Y dimana anggota himpunan A berada pada sumbu X dan anggota himpunan B berada pada sumbu Y. Kedua anggota himpunan ini dihubungkan dengan titik atau sering dikenal dengan nama noktah.

Sebuah bidang Cartesian adalah grafik dengan satu sumbu x dan satu sumbu y. Inilah alasan mengapa kadang-kadang disebut grafik X Y. Kedua sumbu ini saling tegak lurus satu sama lain, lalu titik asal (0) berada tepat di tengah grafik.

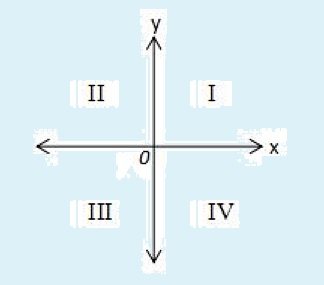
Angka di sisi kanan nol pada sumbu x (horizontal) menampilkan nilai positif, sedangkan angka di sisi kiri nol adalah negatif. Untuk sumbu y (vertikal), angka di bawah nol bernilai negatif dan angka di atas bernilai positif. Lebih jelasnya, lihat gambar dibawah ini :

Umumnya, diagram Kartesius memiliki kuadran. Hal tersebut memberikan banyak kemudahan dalam penyelesaian trigonometri. Pada contoh gambar diagram kartesius diatas, setidaknya Anda akan menemukan empat kuadran yang di antaranya sebagai berikut.

• Kuadran pertama yang terletak di sisi kanan atas
• Kuadran kedua yang terletak di sisi kiri atas.
• Kuadran ketiga yang terletak di sis kiri bawah.
• Kuadran keempat yang terletak di sis kanan bawah.

Selain mengenal kuadran, dalam diagram Kartesius ada pula yang disebut sebagai ordinat dan absis. Keduanya mengacu pada pasangan berurutan pada bidang Kartesius. Absis merupakan nilai x atau angka pertama dalam pasangan berurutan, sedangkan ordinat adalah nilai y atau angka kedua.

Misalnya, sebuah diagram Kartesius menunjukkan titik (-3,1), maka ini artinya -3 adalah absis dan ordinatnya merujuk pada angka 1. Prinsip dasarnya selalu berpatokan pada (x, y), di mana poin pertama yang Anda dapatkan akan selalu berada di bagian X dari grafik, dan angka kedua akan selalu mengisi posisi Y.

Fungsi Diagram Kartesius

Fungsi diagram kartesius (Cartesius) yang utama adalah untuk menentukan koordinat suatu titik pada bidang datar menggunakan dua buah bilangan yang biasa disebut koordinat x(absis) dan koordinat y (ordinat).

Dalam penerapannya, diagram Kartesius memiliki banyak manfaat, terutama dalam cabang ilmu matematika. Namun secara umum, berikut beberapa fungsi yang perlu Anda pahami.

• Membuat grafik fungsi persamaan Aljabar

Dalam matematika, akan ada suatu momen ketika Anda harus membuat grafik dari persamaan aljabar, untuk sepenuhnya memahami dan menafsirkan karakteristiknya. Persamaan dalam bentuk y = f (x), di mana y merupakan fungsi dari x, Anda dapat menggambarnya pada diagram Kartesius.

Untuk setiap nilai x, Anda dapat menentukan nilai y dari persamaan tersebut, dan oleh karena itu, setiap titik pada grafik (x, y) dapat diplot.

• Menunjang keterampilan membaca peta

Saat ini, Anda memang dimungkinkan menemukan jalan ke mana saja secara virtual, berkat navigasi satelit dan aplikasi seluler pendukung. Namun, memiliki keterampilan membaca peta dinilai masih sangat berguna.

Suatu hari, tidak menutup kemungkinan Anda akan menemukan diri dalam situasi di mana tidak ada sinyal seluler sama sekali atau kehabisan daya baterai ponsel.

Cara Membuat Diagram Kartesius

Setelah mengetahui definisi dan fungsi diagram Kartesius, tentu berikutnya Anda pun harus paham bagaimana cara membuatnya. Berikut langkah-langkah sederhana yang bisa dicoba.

• Tentukan nilai x

Nilai x tersebut biasanya berguna untuk dimasukkan ke dalam persamaan, misalnya f (x) = x² – 2. Biasanya, orang cenderung lebih memilih bilangan bulat karena lebih mudah diselesaikan. Bilangan bulat tersebut kemudian ditambah nol dan negatif seperti -2, -1, 0, 1, 2, dan seterusnya.

• Buat beberapa koordinat (x, y)

Seperti telah disinggung sebelumnya, diagram Kartesius selalu ditempati oleh x di posisi pertama dan y pada posisi kedua.

• Gambarkan titik-titik pada bidang Kartesius

Titik-titik tersebut dimaksudkan untuk memudahkan Anda dalam membuat plot dari persamaan yang telah ada sebelumnya.

• Gambar kurva atau garis

Selanjutnya, Anda perlu menggambarkan kurva atau garis setelah menciptakan titik-titik pada bidang Kartesius. Tujuannya untuk mempertegas visual sehingga menjadi sebuah diagram yang utuh.

Contoh Soal Diagram Kartesius

1. Ambillah contoh soal, di mana Anda diminta untuk menggambarkan grafik dari persamaan y = x² – 2 pada bidang Kartesius. Untuk menjawabnya, pahami langkah berikut ini.

Pembahasan :

• Pilih nilai x.

Terserah Anda ingin memilih nilai apa, tetapi sebaiknya gunakan angka yang mudah dihitung.

• Masukkan nilai x pada persamaan.

Untuk melakukan ini, Anda harus mengganti “x” dalam persamaan y = x² – 2, dengan angka yang sudah dipilih sebelumnya. Misalnya, -2, -1, 0, 1, 2. Maka, nilainya menjadi 2, -1, -2, -1, 2.

• Buat tabel

Ini hanya opsional, tetapi kehadirannya cukup membantu untuk memperjelas angka pada sumbu x dan y.

• Plot titiknya

Berpedoman pada angka sebelumnya, berarti titik-titik yang tersedia ada (-2, 2), (-1, -1), (0, -2), (1, -1), dan (2, 2).

• Gambar grafik atau garis dari titik-titik tersebut.

Hasil akhirnya akan jadi seperti gambar diagram kartesius berikut ini :

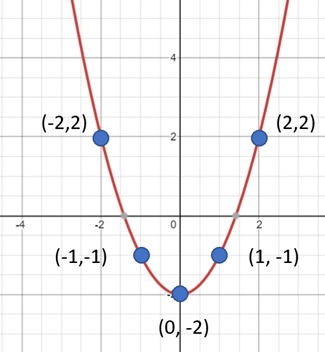
Apabila Anda membuat sebuah diagram Kartesius, jangan lupa untuk selalu berpedoman pada sumbu (x, y). Dari sini, persamaan rumit sekalipun bisa diselesaikan karena telah memahami konsepnya.

2. Jika diketahui titik P adalah (3, 2) dan titik Q adalah (15, 13). Koordinat relatif titik Q terhadap P yang benar adalah. . . .

a. (12, 10)
b. (12, 9)
c. (12, 11)
d. (18, 12)
e. (18, 10)

Pembahasan :

Untuk mencari koordinat relatif antara titik Q ke titik P bisa kita gunakan rumus perhitungan berikut:

•  Absis Q dikurangi absis P
• Ordinat Q dikurangi ordinat P

Maka didapatkan hasil koordinat relatif Q terhadap P yaitu (15 – 3 , 13 – 2) = (12, 11)

Dalam opsi diatas jawaban yang benar adalah opsi C yaitu (12, 11)

3. Diketahui terdapat beberapa titik titik dalam koordinat cartesius sebagai berikut :

1. (-4,7)
2. (-54,2)
3. (3,3)
4. (85,-77)
5. (2,3)

Tentukan letak Kuadran titik titik koordinat diatas?

Pembahasan:

Berdasarkan diagram cartesius, berikut letak titik titik koordinat diatas :

1. (-4,7) Terletak pada kuadran II
2. (-54,2) Terletak pada kuadran III
3. (3,3) Terletak pada kuadran I
4. (85,-77) Terletak pada kuadran IV
5. (2,3) Terletak pada kuadran I

Demikianlah ulasan materi mengenai diagram cartesius yang bisa wikielektronika.com ulas untuk teman teman semuanya. Semoga materi diatas bisa menambah wawasan dan membantu teman teman dalam mempelajari materi koordinat cartesius di sekolah.