√ Nilai Mutlak: Pengertian, Konsep Dasar, Sifat & Contoh Soal

Nilai Mutlak Adalah?☑️ Penjelasan lengkap mengenai pengertian, sifat sifat, serta contoh soal persamaan & pertidaksamaan nilai mutlak☑️

Nilai mutlak akan dipelajari di dalam salah satu materi dari mata pelajaran matematika ketika Anda baru memasuki SMA. Nilai mutlak ini pastinya bisa digunakan untuk menyelesaikan berbagai persoalan dalam matematika.

Untuk dapat mengetahui dengan lebih banyak lagi tentang materi tersebut, maka simaklah berbagai hal di bawah ini yang membahas tentang sifat, persamaan dan pertidaksamaan nilai mutlak.

Baca Cepat :

Pengertian Nilai Mutlak

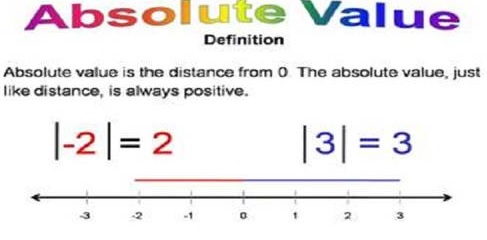
Menurut ilmu Matematika, pengertian nilai mutlak adalah nilai suatu bilangan real tanpa adanya tanda positif (+) ataupun negatif (-). Berapapun besar kecilnya nilai suatu bilangan, nilai mutlaknya tidak akan pernah bernilai negatif (-).

Sebagai contoh nilai mutlak bilangan 4 ( ditulis |4| ) adalah 4, angka empat didapatkan dari jarak antara angka 0 dengan angka 4 yakni berjarak 4 angka. Sehingga pertanyaan berapakah nilai mutlak suatu bilangan sama artinya dengan berapakah jarak angka 0 dengan angka yang ditanyakan tersebut.

Pengertian dari nilai mutlak merupakan salah satu hal yang paling utama untuk Anda ketahui sebelum lebih dalam lagi materi yang berkaitan dengannya. Jika sudah memahami pengertiannya secara baik, maka Anda akan bisa memahami berbagai hal lainnya yang lebih lanjut.

Pengertian Secara Umum

Nilai mutlak adalah suatu jarak diantara bilangan tertentu dengan 0 di garis bilangan real. Dikarenakan jarak, nilainya tidak ada yang negatif. Sehingga, nilai mutlak sendiri bisa juga disebut sebagai nilai yang selalu positif.

Pengertian Dalam Kaidah Bahasa Indonesia

Dalam kaidah Bahasa Indonesia, tentu saja nilai mutlak juga memiliki artian tersendiri. Kata mutlak tersebut dapat diartikan sebagai “seutuhnya”. Sehingga, nilai mutlak adalah nilai yang seutuhnya atau sepenuhnya.

Sedangkan untuk fungsi nilai mutlak adalah fungsi yang variabelnya di dalam tanda mutlak. Untuk lebih mudah dalam memahaminya, simak ulasan contoh dibawah ini.

Fungsi nilai mutlak f(x) = | x | :

X	-3	-2	-1	0	1	2	3
F(x) = [x]	3	2	1	0	1	2	3
(x,y)	(-3, 3)	(-2, 2)	(-1, 1)	(0, 0)	(1, 1)	(2, 2)	(3, 3)

Graﬁk fungsi f(x) = | x | :

Dari grafik fungsi diatas, maka kita dapatkan f(x) = |x|

Keterangan :

1. Untuk x ≥ 0, graﬁk f(x) = | x | merupakan graﬁk f(x) = x

2. Graﬁk f(x) = | x | tidak pernah di bawah sumbu x

3. Untuk x < 0, f(x) = | x | merupakan f(x) = –x

Konsep Dasar Nilai Mutlak

Terkadang, permasalahan dalam nilai mutlak tidak sesederhana pengertiannya. Konsep nilai mutlak sering dihubungkan dengan aljabar ataupun konsep matematika lainnya yang menjadikannya semakin rumit.

Memutlakkan Bilangan

Pastinya konsep nilai mutlak ini yaitu memutlakkan sebuah bilangan.. Hal ini berarti bahwa Anda menjadikan bilangan itu menjadi positif.

Dinotasikan

Apabila Anda tidak tahu arti dari dinotasikan, maka arti dinotasikan itu dapat dikatakan ditulisakan. Ini berasal dari kata notasi yang berarti sistem penulisan.

Dapat disimpulkan bahwa bilangan yang ingin Anda mutlakkan tersebut negative, maka Anda harus membuatnya positif. Caranya cukup mudah yakni dengan mengalikannya dengan negatif.

Sebagai contoh Nilai mutlak pada bilangan x dinotasikan dengan |x|, yang dapat dideﬁnisikan sebagai berikut :

|x| = Jarak x dari titik nol pada garis bilangan

Sedangkan dalam aturan formal matematika, nilai mutlak X juga bisa didefinisikan dengan persamaan berikut :

| x | = -x Mika x ≥ 0
| x | = -x Mika x < 0

Jarak bilangan -5 dari 0 adalah 5 sehingga |-5| = 5. Jarak 5 dari 0 adalah 5 sehingga |5| = 5.

Dari ilustrasi gambar diatas, dapat kita definisikan sebagai berikut :

Nilai mutlak bilangan positif ataupun nol adalah bilangan itu sendiri dan nilai mutlak bilangan negatif adalah lawan dari bilangan tersebut.

Contohnya:

| 9 | = 9 , | 0 | = 0, | -7 | = -(-7) = 7

Sehingga nilai mutlak tiap bilangan real akan selalu memiliki nilai positif atau nol.

Sifat Nilai Mutlak

Konsep di atas bisa diperluas dalam kondisi yang melibatkan berbagai bentuk aljabar yang ada dalam simbol dari nilai mutlak. Hal itu seperti yang akan dijelaskan dalam sifat-sifat nilai mutlak berikut ini :

Non-negatif |a| 0
Definisi-positif |a| = 0a = 0
Multiplikasi |ab| = |a| |b|
Subaditivitas |a + b| |a| + |b|
Idempotensi ||a|| = |a|
Simetri |−a| = |a|
Identitas tak terlihat |a b| = 0 a = b
Pertidaksamaan segitiga |a b| |a c| + |c b|
Preservasi pembagian |a/b|=|a|/|b| jika b 0
Subaditifitas Setara |a−b|≥||a|−|b||

a. Sifat Perkalian Nilai Mutlak

Apabila A dan B merupakan bentuk-bentuk dari aljabar, tentunya |AB| = |A||B|. Apabila A= –1, maka berdasarkan sifat itu berarti |–B| = |–1||B| = |B|.Sifat tersebut secara umum berlaku dalam sembarang konstanta A.

b. Sifat Persamaan Nilai Mutlak

Apabila X merupakan suatu bentuk dari aljabar serta K adalah bilangan real positif, tentunya |X| = k ini akan mengimplikasikan bahwa X = k atau X = –k.

Persamaan Nilai Mutlak

Persamaan linier nilai mutlak ini sering menjadi materi yang dibingungkan dalam mempelajari materi tentang nilai mutlak. Di bawah ini beberapa penjelasan singkatnya.

Persamaan nilai mutlak ialah nilai mutlak dari angka yang bisa diartikan sebagai jarak angka yang ada di atas titik nol di garis angka tanpa harus memperhatikan tentang arahnya.

Seperti yang telah dinyatakan pada sifat persamaan nilai mutlak di atas, sifat nilai mutlak hanya bisa diterapkan sesudah Anda mengisolasi simbol dari nilai mutlak di satu ruas.

Bentuk umum dari persamaan nilai mutlak bisa anda lihat dibawah ini :

Untuk f(x) dan g(x) fungsi dalam variabel x

|f (x)| = c dengan syarat c ≥ 0
|f (x)| = |g (x)|
|f (x)| = |g (x)| dengan syarat |g (x)| ≥ 0

Contoh Soal Persamaan Nilai Mutlak

Untuk bisa lebih memahami mengenai persamaan nilai mutlak, maka cobalah untuk mengerjakan contoh soal.

1. Tentukan nilai x yang akan memenuhi persamaan nilai mutlak dari |2x+1|=5.

Jawaban :

Cara 1 : Cara yang pertama ini Anda dapat memakai sifat berupa persamaan nilai mutlak linear 1 variabel, yakni ax+b=c dan –(ax+b)=c

Cara 2 : Cara yang kedua ini Anda bisa memakai sifat persamaan nilai mutlak linear 1 variabel, yaitu bila |f(x)|=c maka f(x)=-c atau f(x)=c

2. Tentukan himpunan penyelesaian dari bilangan berikut ini |2x – 7| = 3

Jawaban :

|2x – 7| = 3 ( 2x – 7 = 3 ataupun 2x – 7 = -3)

|2x – 7| = 3 ( 2x = 10 ataupun 2x = 4)

|2x – 7| = 3 ( x = 5 ataupun x = 2) Maka, HP = {2, 5}

Jadi himpunan penyelesaian dari bilangan |2x – 7| = 3 adalah {2, 5}

3. Tentukan himpunan penyelesaian dari bilangan berikut ini |2x – 1| = |x + 4|

Jawaban :

|2x – 1| = |x + 4|

2x – 1 = x + 4 ataupun 2x – 1 = -(x + 4)

x = 5 ataupun 3x = -3 x = 5 ataupun x = -1

HP = (-1, 5)

Jadi himpunan penyelesaian dari bilangan |2x – 1| = |x + 4| adalah (-1, 5)

Pertidaksamaan Nilai Mutlak

Pertidaksamaan linier nilai mutlak merupakan kalimat matematika yang terbuka dan memuat ungkapan berupa <,>, ≤, atau ≥. Berikut ini beberapa hal mengenai pertidaksamaan nilai mutlak.

Pertidaksamaan nilai absolut atau pertidaksamaan nilai mutlak ialah suatu pertidaksamaan yang senantiasa benar dalam setiap nilai pengganti dari variabelnya.

Untuk pertidaksamaan tersebut disebut juga dengan ketidaksamaan, serta pastinya ketidaksamaan ini menjadi kalimat matematika yang tertutup.

Sifat pertidaksamaan nilai mutlak adalah apabila P(x), R(x), dan Q (x) merupakan beberapa ungkapan dalam x, untuk seluruh harga x, P(x), R(x), dan Q(x) yang real, maka kalimat terbuka berupa P(x) < Q(x) merupakan ekuivalen dengan kalimat-kalimat terbuka.

Misalkan jika |x| adalah nilai mutlak x dan a suatu bilangan real, maka didapatkan persamaan a. Jika |x| ≤ a maka –a ≤ f(x) ≤ a dan jika |x| ≥ a maka x ≤ –a atau ≥ a

Contoh Soal Pertidaksamaan Nilai Mutlak

Karena sudah paham tentang persamaan nilai mutlak, maka coba juga memahami pertidaksamaan nilai mutlak. Kerjakan contoh soal berikut ini

1. Tentukanlah himpunan penyelesaian dari pertidaksamaan nilai mutlak dari |5x+10|≥20.

Jawaban :

Menggunakan Sifat Pertidaksamaan Nilai Mutlak

Dengan menggunakan sifat pertidaksamaan Nilai Mutlak, persamaan diatas dapat kita definisikan dengan 5x+10≥20, 5x≥10, x≥2.

Lalu, dilanjutkan lagi menjadi 5x+10≤-20, 5x≤-30, x≤-6.

Jadi, himpunan penyelesaian dari |5x+10|≥20t adalah x≥2 serta x≤-6.

2. Tentukan himpunan penyelesaian dari bilangan |4x + 2| ≥ 6

Jawaban :

Berdasarkan sifat pertidaksamaan nilai mutlak kita daparkan :

|4x + 2| ≥ 6 4x + 2 ≤ -6 atau 4x + 2 ≥ 6

|4x + 2| ≥ 6 4x ≤ -8 atau 4x ≥ 4

|4x + 2| ≥ 6 x ≤ -2 atau x ≥ 1

HP = {x ≤ -2 atau x ≥ 1}

Jadi, himpunan penyelesaian dari bilangan |4x + 2| ≥ 6 adalah {x ≤ -2 atau x ≥ 1}

3. Tentukan himpunan penyelesaian dari persamaan |2x – 1| < 7

Jawaban :

|2x – 1| < 7 -7 < 2x – 1 < 7

|2x – 1| < 7 -6 < 2x < 8

|2x – 1| < 7 -3 < x < 4

HP = {-3 < x < 4}

Jadi, himpunan penyelesaian dari persamaan |2x – 1| < 7 adalah {-3 < x < 4}

4. Tentukan himpunan penyelesaian dari bilangan berikut ini |3x – 2| ≥ |2x + 7|

Jawaban :

|3x – 2| ≥ |2x + 7|

3x – 2 ≤ -(2x + 7) atau 3x – 2 ≥ 2x + 7

5x ≤ -5 atau x ≥ 9

x ≤ -1 atau x ≥ 9

HP = {x ≤ -1 atau x ≥ 9}

Jadi, himpunan penyelesaian dari persamaan |3x – 2| ≥ |2x + 7| adalah {x ≤ -1 atau x ≥ 9}

Materi Pembelajaran Lainnya :

Besaran Pokok	Besaran Turunan
Konversi Sistem Bilangan	Besaran Vektor dan Skalar

Nah, itulah beberapa hal mengenai nilai mutlak yang bisa wikielektronika.com ulas. Jika bisa memahami materi tersebut dengan baik, tentu banyak manfaat yang bisa diperoleh. Selamat belajar dan semoga sukses selalu!