b. Jika nilai probabilitas variabel independen lebih kecil (<) dari 0,05 maka terjadi heteroskedastisitas.
- Uji Autokorelasi
Model regresi yang baik seharusnya tidak memiliki autokorelasi. Namun, uji ini dilaksanakan hanya jika penelitian berorientasi data series. Pengujian ini hanya digunakan dalam penelitian data series, di mana model regresi yang baik bebas dari autokorelasi.
Ghozali (2017:121) menyatakan bahwa uji autokorelasi bertujuan untuk menguji apakah dalam model regresi linier ada korelasi antara kesalahan pengganggu pada periode t tabel dengan kesalahan pengganggu pada periode t-1 (sebelumnya).
Sederhananya, Autokorelasi berguna untuk mengecek apakah ada hubungan antara kesalahan pengganggu pada periode t dengan periode sebelumnya (t-1).
Autokorelasi muncul karena observasi yang berurutan sepanjang waktu berkaitan satu sama lainnya. Salah satu uji formal yang paling popular untuk mendeteksi autokorelasi adalah uji pada tabel Durbin-Watson (DW), dasar pengambilan keputusan ada tidaknya autokorelasi adalah:
- Bila nilai DW terletak diantara batas atas atau upper bound (dU) dan (4-dU) maka koefisien autokorelasinya sama dengan nol, berarti tidak ada autokorelasi.
- Bila DW lebih rendah dari batas bawah atau lower bound (dL) maka koefisien autokorelasi lebih besar daripada nol, berarti ada autokorelasi positif.
- Bila DW lebih besar dari (4-dU) maka koefisien autokorelasinya lebih kecil daripada nol, berarti ada autokorelasi.
- Bila nilai DW terletak antara batas atas (dU) dan bawah (dL) atau DW terletak antara (40dU) dan (4-dL) maka hasilnya tidak dapat disimpulkan.
- Uji Linieritas
Uji linearitas dipergunakan untuk melihat apakah model yang dibangun mempunyai hubungan linear atau tidak. Pengujian ini jarang digunakan dalam beberapa studi karena model biasanya dibangun atas dasar studi teoritis bahwa hubungan antara variabel independen dan variabel dependen adalah linier.
Hubungan antar variabel yang secara teoritis tidak hubungan linear tidak dapat dianalisis dengan regresi linier, seperti masalah elastisitas.
Jika ada hubungan antara dua variabel yang belum diketahui apakah linear atau tidak, uji linearitas tidak dapat digunakan untuk memberikan adjustment bahwa hubungan tersebut bersifat linear atau tidak.
Uji linearitas digunakan untuk mengkonfirmasi apakah sifat linear antara dua variabel yang diidentifikasi dalam teori sesuai dengan hasil pengamatan. Tes linearitas dapat dilakukan dengan menggunakan uji DurbinWatson, tes Ramsey atau tes pengali Lagrange.
Contoh Uji Asumsi Klasik
Uji asumsi klasik dilakukan untuk mengetahui apakah pemodelan regresi linear berganda adalah tepat. Dengan begitu, Anda bisa menganalisis lebih mendalam tanpa terganggu oleh data yang mungkin bias. Berikut untuk contoh pengujian data menggunakan uji asumsi klasik yang bisa anda simak :
1. Contoh Uji Asumsi Klasik dengan SPSS
Uji asumsi klasik dapat ditemukan dengan bantuan SPSS, sebuah software statistik. Ambillah contoh uji normalitas. Pengujian ini dapat dilaksanakan dengan menggunakan alat One Sample Kolmogorov Smirnov lewat SPSS.
Jika nilai signifikansi melebihi 0,05 atau 5%, artinya data terdistribusi normal. Adapun langkah-langkah yang harus ditempuh adalah sebagai berikut.
- Tabulasi data dengan meng-inputkan data penelitian Anda pada worksheet SPSS atau jika ingin cepat bisa membuatnya terlebih dahulu lewat Excel. Kemudian, salin dan tempel dari Excel ke SPSS.
- Lakukan uji normalitas dan heteroskedastisitas terlebih dahulu.
- Uji autokorelasi serta multikolinearitas
Perlu dipahami, bahwasanya uji autokorelasi hanya berlaku apabila penelitian memanfaatkan jenis data time series. Di lain pihak, uji multikolinearitas juga baru dijalankan bila ada lebih dari satu variabel independen.
Dibawah ini merupakan contoh soal dilengkapi pembahasannya mengenai uji asumsi klasik SPSS.
Contoh Soal
Contoh soal pada kasus ini mengangkat kasus permintaan ayam di Amerika selama periode 1960-1982 yang bersumber dari jurnal penelitian Mahasiswa Universitas Negeri Semarang (2010) bernama Andryan Setyadharma dengan mengutip penelitian dari (Gujarati, 1995: 228).
Berikut tabel data Permintaan Ayam di AS, 1960-1982. (Source : http://akuntansi.unnes.ac.id/wp-content/uploads/2010/05/Uji-Asumsi-Klasik-dengan-SPSS-16.0.pdf)
| Tahun | Y | X2 | X3 | X4 | X5 |
| 1960 | 27.8 | 397.5 | 42.2 | 50.7 | 78.3 |
| 1961 | 29.9 | 413.3 | 38.1 | 52 | 79.2 |
| 1962 | 29.8 | 439.2 | 40.3 | 54 | 79.2 |
| 1963 | 30.8 | 459.7 | 39.5 | 55.3 | 79.2 |
| 1964 | 31.2 | 492.9 | 37.3 | 54.7 | 77.4 |
| 1965 | 33.3 | 528.6 | 38.1 | 63.7 | 80.2 |
| 1966 | 35.6 | 560.3 | 39.3 | 69.8 | 80.4 |
| 1967 | 36.4 | 624.6 | 37.8 | 65.9 | 83.9 |
| 1968 | 36.7 | 666.4 | 38.4 | 64.5 | 85.5 |
| 1969 | 38.4 | 717.8 | 40.1 | 70 | 93.7 |
| 1970 | 40.4 | 768.2 | 38.6 | 73.2 | 106.1 |
| 1971 | 40.3 | 843.3 | 39.8 | 67.8 | 104.8 |
| 1972 | 41.8 | 911.6 | 39.7 | 79.1 | 114 |
| 1973 | 40.4 | 931.1 | 52.1 | 95.4 | 124.1 |
| 1974 | 40.7 | 1021.5 | 48.9 | 94.2 | 127.6 |
| 1975 | 40.1 | 1165.9 | 58.3 | 123.5 | 142.9 |
| 1976 | 42.7 | 1349.6 | 57.9 | 129.9 | 143.6 |
| 1977 | 44.1 | 1449.4 | 56.5 | 117.6 | 139.2 |
| 1978 | 46.7 | 1575.5 | 63.7 | 130.9 | 165.5 |
| 1979 | 50.6 | 1759.1 | 61.6 | 129.8 | 203.3 |
| 1980 | 50.1 | 1994.2 | 58.9 | 128 | 219.6 |
| 1981 | 51.7 | 2258.1 | 66.4 | 141 | 221.6 |
| 1982 | 52.9 | 2478.7 | 70.4 | 168.2 | 232.6 |
Variabel yang digunakan terdiri atas :
- Y = konsumsi ayam per kapita
- X2 = pendapatan riil per kapita.
- X3 = harga ayam eceran riil per unit
- X4 = harga babi eceran riil per unit
- X5 = harga sapi eceran riil per unit
Teori ekonomi mikro mengajarkan bahwa permintaan akan suatu barang dipengaruhi oleh pendapatan konsumen, harga barang itu sendiri, harga barang substitusi, dan harga barang komplementer.
Dengan data yang ada, kita dapat mengestimasi fungsi permintaan ayam di AS adalah: Ŷi = b1 + b2 X2 + b3 X3 + b4 X4 + b5 X5 + error
- Langkah 1 : Uji Normalitas SPSS
Lakukan regresi untuk data permintaan ayam di atas. Analyze Regression Linear, akan muncul tampilan sebagai berikut:
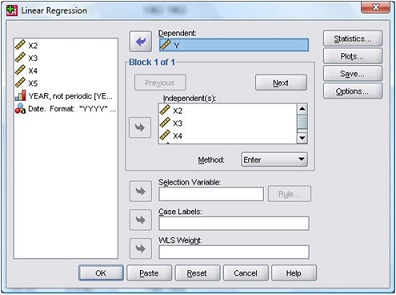
Selanjutnya inputkan variabel Y pada kotak sebelah kiri ke kotak Dependent, dan variabel X2, X3, X4 dan X5 ke kotak Independent(s) dengan mengklik tombol tanda panah. Kemudian pilih Save dan muncul tampilan sebagai berikut:
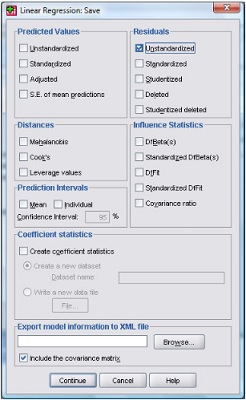
Centang pilihan Unstandardized pada bagian Residuals, kemudian pilih Continue dan pada tampilan awal pilih tombol OK, akan menghasilkan variabel baru bernama Unstandardized Residual (RES_1). Selanjutnya Analyze -> Descriptive Statistics -> Descriptives akan muncul tampilan sebagai berikut:
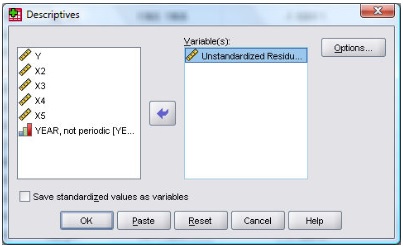
Masukkan variabel Unstandardized Residual (RES_1) ke kotak sebelah kiri, selanjutnya pilih Options yang hasilnya seperti dibawah ini :
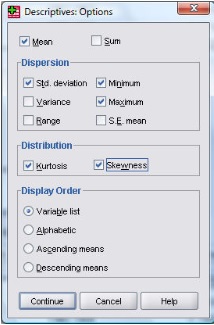
Centang pilihan Kurtosis dan Skewness dan kemudian Continue dan pada tampilan awal pilih OK. Hasilnya sebagai berikut :
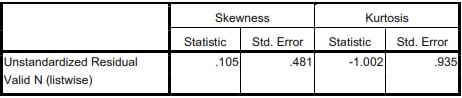
Terlihat bahwa rasio skewness = 0,105/ 0,481 = 0,218; sedang rasio kurtosis = -1,002/ 0,935 = -1,071. Karena rasio skewness dan rasio kurtosis berada di antara –2 hingga +2, maka dapat disimpulkan bahwa distribusi data adalah normal.
- Langkah 2 : Uji Autokorelasi
Lakukan regresi untuk data permintaan ayam di atas seperti pada Uji Normalitas. Setelah itu pilih Statistics akan muncul tampilan seperti di bawah ini. Kemudian centang pilihan Durbin-Watson setelah itu pilih tombol Continue, pada tampilan selanjutnya pilih OK.