Uji asumsi klasik adalah?☑️ Berikut pengertian menurut para ahli plus Contoh uji asumsi klasik menggunakan SPSS dan Eviews☑️
Uji asumsi klasik biasanya dipakai untuk mengecek apakah dalam suatu model penelitian regresi linear Ordinary Least Square memuat persoalan terkait asumsi klasik.
Umumnya, ini dibutuhkan ketika Anda hendak memanfaatkan analisis regresi berganda di mana harus memenuhi sejumlah asumsi agar menghasilkan kesimpulan yang valid.
Pengertian Uji Asumsi Klasik

Menurut (Ghozali 2018), pengertian uji asumsi klasik adalah metode statistik pada analisis regresi linier berganda yang bertujuan untuk menilai apakah terdapat masalah asumsi klasik atau tidak pada model regresi linear Ordinary Least Square (OLS).
Tujuan dari uji asumsi klasik adalah untuk menilai parameter penduga yang digunakan sahih dan tidak bias. Selain itu, uji asumsi klasik juga memiliki fungsi untuk mengetahui apakah model regresi benar-benar menunjukkan hubungan yang signifikan dan representatif ataukah tidak
Asumsi klasik kerap dipakai untuk meninjau apakah dalam suatu model penelitian Ordinary Least Square (OLS) ditemukan persoalan terkait asumsi klasik, seperti multikolinearitas, normalitas, autokorelasi, hingga heteroskedastisitas.
Namun, jauh sebelum itu, Anda perlu memahami apa sebenarnya yang dimaksud model penelitian Ordinary Least Square (OLS)?
Dalam bahasa Indonesia, OLS disebut juga metode perhitungan kuadrat terkecil. Ini mengasumsikan bahwa analisis cocok dengan model hubungan antara satu atau lebih variabel penjelas dan variabel hasilnya kontinu.
regresi OLS sendiri terbagi menjadi 2 macam, yaitu: regresi linear berganda dan juga regresi linear sederhana. Sebuah analisis regresi yang tidak berdasarkan pada OLS ini tidak memerlukan persyaratan uji asumsi klasik, misalnya pada pengujian regresi logistic serta pengujian regresi ordinal.
Dengan adanya dua jenis yang berbeda pada regresi linear, maka syarat atau asumsi klasik pada regresi linear juga ada dua macam, diantaranya sebagai berikut :
- Uji Asumsi Klasik Pada Regresi Linear Sederhana
Asumsi klasik pada regresi linear sederhana antara lain:
a. Data interval atau rasio
b. linearitas
c. normalitas
d. heteroskedastisitas
e. Outlier
f. Autokorelasi (Hanya untuk data time series atau runtut waktu).
- Uji Asumsi Klasik Pada Regresi Linear Berganda
Asumsi klasik pada regresi linear berganda antara lain:
a. Data interval atau rasio
b. linearitas
c. normalitas
d. heteroskedastisitas
e. Outlier
f. Multikollinearität
g. Autokorelasi (Hanya untuk data time series atau runtut waktu).
Konsep Dasar Uji Asumsi Klasik

Setidaknya ada empat macam konsep dasar uji asumsi klasik yang umum digunakan dalam model penelitian regresi linear. Uji asumsi klasik tidak boleh dilakukan sebarangan sebab ada aturan urutan tersendiri. Berikut langkah-langkah yang perlu Anda laksanakan.
- Uji Normalitas
Ini untuk memastikan bahwa data Anda terdistribusi normal ataukah tidak. Keberadaannya adalah wajib dalam sebuah penelitian. Uji normalitas merupakan model regresi yang baik harus memenuhi distribusi normal.
Ghozali (2017:145) menyatakan bahwa uji normalitas bertujuan untuk menguji apakah dalam model regresi, variabel pengganggu atau residual memiliki distribusi normal. Model regresi yang dianggap baik adalah memiliki distribusi normal atau mendekati normal.
Uji statistik yang digunakan untuk menilai normalitas dalam penelitian ini adalah uji Jarque Bera (JB) dengan histogram-normality test. Dengan tingkat signifikansi 5%, indikator yang digunakan untuk pengambilan keputusan bahwa data tersebut terdistribusi normal atau tidak adalah sebagai berikut:
a. Apabila nilai probabilitas lebih besar (>) dari 0,05 maka data terdistribusi secara normal.
b. Apabila nilai probabilitas lebih kecil (<) dari 0,05 maka data tidak terdistribusi secara normal.
- Uji Multikolinearitas
Multikolinearitas adalah hubungan linier antar variabel bebas. Adanya multikolinearitas dalam penelitian memberikan efek tingginya variabel suatu pada sampel. Ini berarti telah terjadi standar error yang besar. Jadi regresi seharusnya tidak memuat gejala multikolinearitas.
Tujuan pemakaiannya untuk mengecek ada atau tidaknya korelasi antar variabel. Namun, uji multikolinearitas baru dilaksanakan jika terdapat lebih dari satu variabel independen.
Ghozali (2017:71) menyatakan bahwa uji multikolinearitas bertujuan untuk menguji apakah dalam model regresi terdapat korelasi yang tinggi atau sempurna antar variabel independen.
Model regresi yang baik seharusnya tidak ada korelasi diantara variabel. Bila ada korelasi yang tinggi diantara variabel bebasnya, maka hubungan antara variabel bebas terhadap variabel terikat menjadi terganggu.
Ghozali (2017:73) menyatakan dengan tingkat signifikansi 90%, adanya multikolinearitas antar variabel independen dapat dideteksi dengan menggunakan matriks korelasi dengan ketentuan sebagai sebagai berikut:
a. Jika nilai matriks korelasi antar dua variabel independen lebih besar dari (>) 0,90 maka terdapat multikolinearitas.
b. Jika nilai matriks korelasi antar dua variabel independen lebih kecil (<) 0,90 maka tidak terdapat multikolinearitas.
- Uji Heteroskedastisitas
Pengujian yang kedua ini dilakukan dalam rangka memastikan apakah model ada ketidaknyamanan varian residual antar pengamat dalam suatu model regresi.
Model regresi yang baik tidak menimbulkan variasi berbeda antara lintas pengamat. Dalam hal ini, sebuah penelitian semestinya tidak mendeteksi adanya heteroskedastisitas.
Ghozali (2017:85) menyatakan bahwa uji heteroskedastisitas bertujuan untuk menguji apakah dalam model regresi terjadi ketidaksamaan varians dari residual satu pengamatan ke pengamatan lain.
Jika varians dari residual satu pengamatan ke pengamatan yang lain konstan maka disebut homoskedastisitas dan jika berbeda maka disebut heteroskedastisitas. Model regresi yang dianggap baik adalah residual satu pengamatan ke pengamatan lain yang konstan atau homoskedastisitas atau tidak terjadi heteroskedastisitas.
Uji statistik yang digunakan untuk menilai heteroskedastisitas dalam penelitian ini adalah uji Breusch Pagan . Ghozali (2017:90) menyatakan bahwa uji Breusch Pagan dapat dilakukan dengan meregres nilai absolute residual terhadap variabel independen lain. Dengan tingkat signifikansi 5%, adanya heteroskedastisitas dapat diketahui dengan kriteria sebagai berikut:
a. Jika nilai probabilitas variabel independen lebih besar (>) dari 0,05 maka tidak terjadi heteroskedastisitas.
b. Jika nilai probabilitas variabel independen lebih kecil (<) dari 0,05 maka terjadi heteroskedastisitas.
- Uji Autokorelasi
Model regresi yang baik seharusnya tidak memiliki autokorelasi. Namun, uji ini dilaksanakan hanya jika penelitian berorientasi data series. Pengujian ini hanya digunakan dalam penelitian data series, di mana model regresi yang baik bebas dari autokorelasi.
Ghozali (2017:121) menyatakan bahwa uji autokorelasi bertujuan untuk menguji apakah dalam model regresi linier ada korelasi antara kesalahan pengganggu pada periode t tabel dengan kesalahan pengganggu pada periode t-1 (sebelumnya).
Sederhananya, Autokorelasi berguna untuk mengecek apakah ada hubungan antara kesalahan pengganggu pada periode t dengan periode sebelumnya (t-1).
Autokorelasi muncul karena observasi yang berurutan sepanjang waktu berkaitan satu sama lainnya. Salah satu uji formal yang paling popular untuk mendeteksi autokorelasi adalah uji pada tabel Durbin-Watson (DW), dasar pengambilan keputusan ada tidaknya autokorelasi adalah:
- Bila nilai DW terletak diantara batas atas atau upper bound (dU) dan (4-dU) maka koefisien autokorelasinya sama dengan nol, berarti tidak ada autokorelasi.
- Bila DW lebih rendah dari batas bawah atau lower bound (dL) maka koefisien autokorelasi lebih besar daripada nol, berarti ada autokorelasi positif.
- Bila DW lebih besar dari (4-dU) maka koefisien autokorelasinya lebih kecil daripada nol, berarti ada autokorelasi.
- Bila nilai DW terletak antara batas atas (dU) dan bawah (dL) atau DW terletak antara (40dU) dan (4-dL) maka hasilnya tidak dapat disimpulkan.
- Uji Linieritas
Uji linearitas dipergunakan untuk melihat apakah model yang dibangun mempunyai hubungan linear atau tidak. Pengujian ini jarang digunakan dalam beberapa studi karena model biasanya dibangun atas dasar studi teoritis bahwa hubungan antara variabel independen dan variabel dependen adalah linier.
Hubungan antar variabel yang secara teoritis tidak hubungan linear tidak dapat dianalisis dengan regresi linier, seperti masalah elastisitas.
Jika ada hubungan antara dua variabel yang belum diketahui apakah linear atau tidak, uji linearitas tidak dapat digunakan untuk memberikan adjustment bahwa hubungan tersebut bersifat linear atau tidak.
Uji linearitas digunakan untuk mengkonfirmasi apakah sifat linear antara dua variabel yang diidentifikasi dalam teori sesuai dengan hasil pengamatan. Tes linearitas dapat dilakukan dengan menggunakan uji DurbinWatson, tes Ramsey atau tes pengali Lagrange.
Contoh Uji Asumsi Klasik
Uji asumsi klasik dilakukan untuk mengetahui apakah pemodelan regresi linear berganda adalah tepat. Dengan begitu, Anda bisa menganalisis lebih mendalam tanpa terganggu oleh data yang mungkin bias. Berikut untuk contoh pengujian data menggunakan uji asumsi klasik yang bisa anda simak :
1. Contoh Uji Asumsi Klasik dengan SPSS
Uji asumsi klasik dapat ditemukan dengan bantuan SPSS, sebuah software statistik. Ambillah contoh uji normalitas. Pengujian ini dapat dilaksanakan dengan menggunakan alat One Sample Kolmogorov Smirnov lewat SPSS.
Jika nilai signifikansi melebihi 0,05 atau 5%, artinya data terdistribusi normal. Adapun langkah-langkah yang harus ditempuh adalah sebagai berikut.
- Tabulasi data dengan meng-inputkan data penelitian Anda pada worksheet SPSS atau jika ingin cepat bisa membuatnya terlebih dahulu lewat Excel. Kemudian, salin dan tempel dari Excel ke SPSS.
- Lakukan uji normalitas dan heteroskedastisitas terlebih dahulu.
- Uji autokorelasi serta multikolinearitas
Perlu dipahami, bahwasanya uji autokorelasi hanya berlaku apabila penelitian memanfaatkan jenis data time series. Di lain pihak, uji multikolinearitas juga baru dijalankan bila ada lebih dari satu variabel independen.
Dibawah ini merupakan contoh soal dilengkapi pembahasannya mengenai uji asumsi klasik SPSS.
Contoh Soal
Contoh soal pada kasus ini mengangkat kasus permintaan ayam di Amerika selama periode 1960-1982 yang bersumber dari jurnal penelitian Mahasiswa Universitas Negeri Semarang (2010) bernama Andryan Setyadharma dengan mengutip penelitian dari (Gujarati, 1995: 228).
Berikut tabel data Permintaan Ayam di AS, 1960-1982. (Source : http://akuntansi.unnes.ac.id/wp-content/uploads/2010/05/Uji-Asumsi-Klasik-dengan-SPSS-16.0.pdf)
| Tahun | Y | X2 | X3 | X4 | X5 |
| 1960 | 27.8 | 397.5 | 42.2 | 50.7 | 78.3 |
| 1961 | 29.9 | 413.3 | 38.1 | 52 | 79.2 |
| 1962 | 29.8 | 439.2 | 40.3 | 54 | 79.2 |
| 1963 | 30.8 | 459.7 | 39.5 | 55.3 | 79.2 |
| 1964 | 31.2 | 492.9 | 37.3 | 54.7 | 77.4 |
| 1965 | 33.3 | 528.6 | 38.1 | 63.7 | 80.2 |
| 1966 | 35.6 | 560.3 | 39.3 | 69.8 | 80.4 |
| 1967 | 36.4 | 624.6 | 37.8 | 65.9 | 83.9 |
| 1968 | 36.7 | 666.4 | 38.4 | 64.5 | 85.5 |
| 1969 | 38.4 | 717.8 | 40.1 | 70 | 93.7 |
| 1970 | 40.4 | 768.2 | 38.6 | 73.2 | 106.1 |
| 1971 | 40.3 | 843.3 | 39.8 | 67.8 | 104.8 |
| 1972 | 41.8 | 911.6 | 39.7 | 79.1 | 114 |
| 1973 | 40.4 | 931.1 | 52.1 | 95.4 | 124.1 |
| 1974 | 40.7 | 1021.5 | 48.9 | 94.2 | 127.6 |
| 1975 | 40.1 | 1165.9 | 58.3 | 123.5 | 142.9 |
| 1976 | 42.7 | 1349.6 | 57.9 | 129.9 | 143.6 |
| 1977 | 44.1 | 1449.4 | 56.5 | 117.6 | 139.2 |
| 1978 | 46.7 | 1575.5 | 63.7 | 130.9 | 165.5 |
| 1979 | 50.6 | 1759.1 | 61.6 | 129.8 | 203.3 |
| 1980 | 50.1 | 1994.2 | 58.9 | 128 | 219.6 |
| 1981 | 51.7 | 2258.1 | 66.4 | 141 | 221.6 |
| 1982 | 52.9 | 2478.7 | 70.4 | 168.2 | 232.6 |
Variabel yang digunakan terdiri atas :
- Y = konsumsi ayam per kapita
- X2 = pendapatan riil per kapita.
- X3 = harga ayam eceran riil per unit
- X4 = harga babi eceran riil per unit
- X5 = harga sapi eceran riil per unit
Teori ekonomi mikro mengajarkan bahwa permintaan akan suatu barang dipengaruhi oleh pendapatan konsumen, harga barang itu sendiri, harga barang substitusi, dan harga barang komplementer.
Dengan data yang ada, kita dapat mengestimasi fungsi permintaan ayam di AS adalah: Ŷi = b1 + b2 X2 + b3 X3 + b4 X4 + b5 X5 + error
- Langkah 1 : Uji Normalitas SPSS
Lakukan regresi untuk data permintaan ayam di atas. Analyze Regression Linear, akan muncul tampilan sebagai berikut:
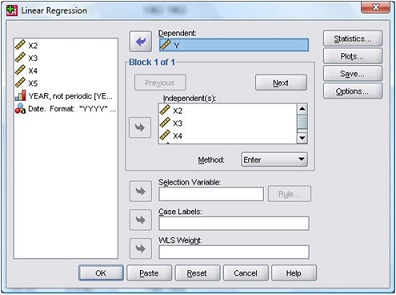
Selanjutnya inputkan variabel Y pada kotak sebelah kiri ke kotak Dependent, dan variabel X2, X3, X4 dan X5 ke kotak Independent(s) dengan mengklik tombol tanda panah. Kemudian pilih Save dan muncul tampilan sebagai berikut:
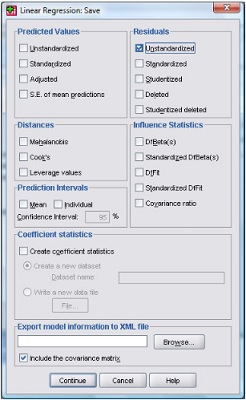
Centang pilihan Unstandardized pada bagian Residuals, kemudian pilih Continue dan pada tampilan awal pilih tombol OK, akan menghasilkan variabel baru bernama Unstandardized Residual (RES_1). Selanjutnya Analyze -> Descriptive Statistics -> Descriptives akan muncul tampilan sebagai berikut:
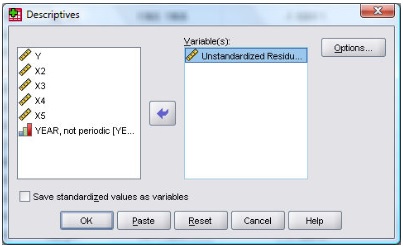
Masukkan variabel Unstandardized Residual (RES_1) ke kotak sebelah kiri, selanjutnya pilih Options yang hasilnya seperti dibawah ini :
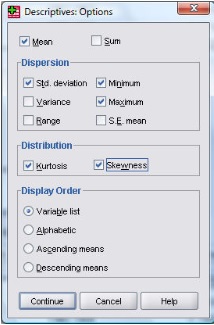
Centang pilihan Kurtosis dan Skewness dan kemudian Continue dan pada tampilan awal pilih OK. Hasilnya sebagai berikut :
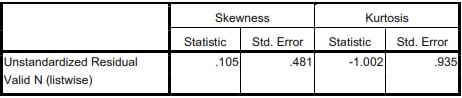
Terlihat bahwa rasio skewness = 0,105/ 0,481 = 0,218; sedang rasio kurtosis = -1,002/ 0,935 = -1,071. Karena rasio skewness dan rasio kurtosis berada di antara –2 hingga +2, maka dapat disimpulkan bahwa distribusi data adalah normal.
- Langkah 2 : Uji Autokorelasi
Lakukan regresi untuk data permintaan ayam di atas seperti pada Uji Normalitas. Setelah itu pilih Statistics akan muncul tampilan seperti di bawah ini. Kemudian centang pilihan Durbin-Watson setelah itu pilih tombol Continue, pada tampilan selanjutnya pilih OK.
Hasil dari perhitungan Durbin-Watson Statistik akan muncul pada tabel Model Summary seperti di bawah ini:
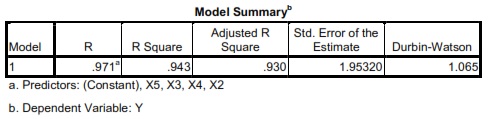
Langkah selanjutnya adalah menetapkan nilai dL dan dU. Caranya adalah dengan menggunakan derajat kepercayaan 5%, sampel (n) yang kita miliki sebanyak 23 observasi, dan variabel penjelas sebanyak 4 maka dapatkan nilai dL dan dU sebesar 1,078 dan 1,660. Maka dapat disimpulkan bahwa model ini memiliki gejala autokorelasi positif.
- Langkah 3 : Uji Multikolinieritas
Lakukan regresi untuk data permintaan ayam di atas seperti pada Uji Normalitas. Setelah itu pilih Statistics kemudian centang pilihan Collinearity Diagnostics setelah itu pilih tombol Continue dan akhirnya pada tampilan selanjutnya pilih OK. Hasilnya sebagai berikut.
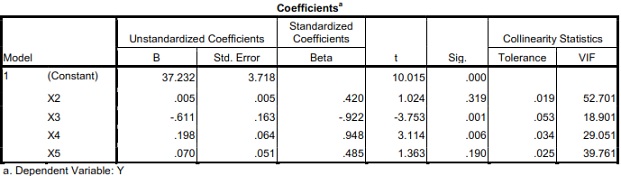
Dari tabel diatas dapat kita simpulkan bahwa seluruh variabel penjelas memiliki nilai VIF lebih besar 10 maka dapat disimpulkan bahwa model regresi ini memiliki masalah Multikolinieritas.
- Langkah 4 : Uji Heteroskedastisitas
Kita sudah memiliki variabel Unstandardized Residual (RES_1) (lihat lagi langkah-langkah uji Normalitas di atas). Selanjutnya pilih Transform -> Compute Variable, akan muncul tampilan sebagai berikut:
Pada kotak Target Variable ketik abresid, pada kotak Function group pilih All dan dibawahnya akan muncul beberapa pilihan fungsi. Pilihlah Abs.
Kemudian klik pada tombol tanda panah arah ke atas, dan masukkan variabel Unstandardized Residual (RES_1) ke dalam kotak Numeric Expression dan tampilannya akan menjadi seperti berikut. Dan pilih OK.
Kemudian dilanjutkan dengan regresi dengan cara, Analyze Regression Linear, akan muncul tampilan sebagai berikut:
Selanjutnya masukkan variabel abresid pada kotak sebelah kiri ke kotak Dependent, dan variabel X2, X3, X4 dan X5 ke kotak Independent(s) dengan mengklik tombol tanda panah dan OK, hasilnya sebagai berikut:
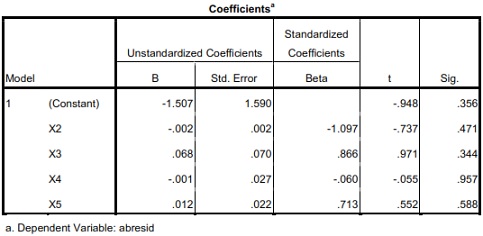
Nilai t-statistik dari seluruh variabel pejelas tidak ada yang signifikan secara statistik, sehingga dapat disimpulkan bahwa model ini tidak mengalami masalah heteroskedastisitas.
2. Contoh Uji Asumsi Klasik dengan EViews
[embedyt] https://www.youtube.com/watch?v=nCzfk-aJJfA[/embedyt]
Sumber Video : Youtube.com via Channel Tabrani Education
Tidak hanya SPSS, ada software lain yang bisa digunakan untuk melakukan uji asumsi klasik. EViews disinyalir sangat kompatibel jika Anda bergelut di bidang ilmu ekonomi. Di sini, Anda bisa melakukan olah data dan panel data. Caranya sebagai berikut.
- Siapkan data yang hendak diolah
- Buka EViews dengan mengeklik File, lalu New, dan Workfile
- Pilih Balanced Panel di bilah Workfile structure type
- Untuk data berbentuk tahunan, klik Annual pada panel Specification
- Ketuk Empty Group di bagian Quick
- Salin data pada worksheet yang tersedia
- Klik Proc, lalu Make Equation
- Klik Specification setelah muncul tampilan Equation Estimator
- Pastikan persamaan regresi berurutan y c x. Di bagian Method, ketuk bilah LS – Least Squared (NLS and ARMA)
- Pilih uji yang ingin dijalankan pada Panel Option, persisnya di Effects specification, lalu Cross section
- Klik Ok dan tunggu hingga hasilnya muncul.
Uji asumsi klasik harus dilaksanakan pada model penelitian regresi. Untungnya, sekarang ini sudah dimudahkan dengan adanya software statistik seperti SPSS dan EViews.
| Contoh Uji Skala Likert | Contoh Uji Hipotesis |
| Contoh Uji Purposive Sampling | Contoh Uji T |
Yang perlu anda catat adalah tidak semua pengujian asumsi klasik harus dilakukan pada analisis regresi linear, sebagai contoh uji multikolienearitas tidak dilakukan pada analisis regresi linear sederhana dan uji autokorelasi tidak perlu diterapkan pada data cross sectional.
Analisis uji asumsi klasik tidaklah juga digunakan dalam SMART PLS. Karena didalam SMART PLS digunakan metode pendekatan Partial Least Square – Structural Equation Modeling (PLS-SEM).
Demikianlah ulasan materi mengenai uji asumsi klasik dalam ilmu statistika yang bisa wikielektronika paparkan. Semoga dapat menjadi refrensi yang baik dalam membantu belajar anda. Terimakasih!
Daftar Pustaka:
Ghozali, I. (2016) Aplikasi Analisis Multivariete Dengan Program IBM SPSS 23. Edisi 8. Semarang: Badan Penerbit Universitas Diponegoro.
http://repository.stei.ac.id/1103/4/BAB%20III.pdf
http://akuntansi.unnes.ac.id/wp-content/uploads/2010/05/Uji-Asumsi-Klasik-dengan-SPSS-16.0.pdf
https://lmsspada.kemdikbud.go.id/pluginfile.php/559849/mod_folder/content/0/PERTEMUAN%205%20UJI%20ASUMSI%20KLASIK.pdf?forcedownload=1
Juliandi A, Irfan, Manurung S. 2014. Metodologi Penelitian Bisnis: Konsep dan Aplikasi. Medan: UMSU Press.