Sistem Bilangan Adalah?☑️ Berikut macam macam sistem bilangan (Real, Desimal, Biner, Oktal, Heksadesimal) & Cara Konversi Bilangan☑️
Dalam ilmu Matematika dikenal istilah sistem bilangan yang banyak diterapkan untuk berbagai hal. Sistem bilangan adalah simbol atau kode yang digunakan untuk mewakili besaran dari sebuah item fisik.
Sistem bilangan ini menggunakan bilangan dasar ataupun basis tertentu. Ada beberapa jenis sistem bilangan yang umumnya dikenal dengan fungsi yang berbeda-beda.
Sistem bilangan memiliki berbagai macam jenis. Masing-masing jenis sistem bilangan itu kemudian masih bisa diubah menjadi sistem bilangan lain dengan cara konversi.
Pengertian Sistem Bilangan

Sistem bilangan adalah metode merepresentasikan Angka pada Garis Angka dengan bantuan seperangkat Simbol dan aturan. Simbol yang dimaksud terdiri dari 0 – 9 yang sering kita kenal dengan nama Angka. Contoh sistem bilangan seperti bilangan asli, bilangan bulat, bilangan desimal, bilangan biner, bilangan rasional dan irasional, dll.
Sistem bilangan juga bisa didefinisikan sebagai cara untuk menuliskan bilangan. Bisa juga dikatakan bahwa sistem bilangan merupakan simbol-simbol yang dipakai untuk menerangkan hal-hal secara lebih detail melalui angka.
Suatu sistem bilangan dipakai guna mewakili sebuah perintah tertentu dalam komputer. Dengan begitu, suatu mesin tertentu atau komputer bisa memahami perintah yang diberikan.
Sistem Angka terdiri dari beberapa jenis berdasarkan nilai dasar untuk digitnya. Umumnya sistem Angka digunakan untuk melakukan perhitungan matematis (ilmiah) maupun perhitungan yang sifat nya tidak baku (non ilmiah).
Lalu apa yang dimaksud dengan angka itu sendiri ? Angka adalah nilai matematika yang digunakan untuk menghitung atau mengukur atau memberi label pada objek. Angka digunakan untuk melakukan perhitungan aritmatika
Sedangkan arti dari bilangan adalah Metode dalam matematika yang digunakan untk sebuah pengukuran maupun pencacahan. Umumnya sebuah bilangan berisi kumpulan angka satuan, puluhan, ratusan, ribuan, dan seterusnya.
Suatu bilangan memiliki banyak variasi lain seperti bilangan genap dan ganjil, bilangan prima dan bilangan komposit. Istilah genap dan ganjil digunakan ketika suatu bilangan habis dibagi 2 atau tidak, sedangkan bilangan prima dan komposit membedakan antara bilangan yang masing-masing hanya memiliki dua faktor dan lebih dari dua faktor.
Macam Macam Sistem Bilangan

Sistem bilangan dibagi menjadi beberapa jenis. Macam macam sistem bilangan yang umumnya dikenal, yaitu sistem bilangan biner, sistem bilangan desimal, sistem bilangan oksal dan sistem bilangan hexadecimal.
-
Sistem Bilangan Biner
Macam sistem bilangan yang pertama adalah sistem bilangan biner. Menurut Wikipedia, sistem bilangan ini disebut juga dengan bilangan berbasis 2 karena hanya terdiri atas 2 simbol, yaitu 0 dan 1. Kegunaan dari bilangan ini adalah untuk merepresentasikan alat yang memiliki dua keadaan operasi dan berlawanan.
Untuk lebih mudah dalam memahaminya, perhatikan contoh soal bilangan biner berikut : Tuliskan angka (14)10 dalam bilangan biner!
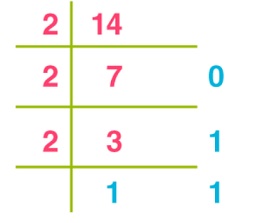
Bisa anda dilihat pada gambar diatas bahwa jawaban soal untuk bilangan biner dari (14)10 adalah ∴ (14)10 = 11102
-
Sistem Bilangan Desimal
Jenis kedua adalah sistem bilangan desimal, yaitu cara menghitung bilangan dengan memakai sepuluh simbol. Sepuluh simbol angka itu mulai dari 0, 1, 2,3 , 4, 5, 6, 7, 8 dan 9. Bilangan ini disebut juga dengan bilangan berbasis 10. Sistem ini tidak cocok jika digunakan pada sistem digital.
Sebagai contoh Bilangan desimal 1457 terdiri dari angka 7 pada posisi satuan, 5 pada posisi puluhan, 4 pada posisi ratusan, dan 1 pada posisi ribuan yang nilainya dapat ditulis sebagai :
(1×103) + (4×102) + (5×101) + (7×100)
(1×1000) + (4×100) + (5×10) + (7×1)
1000 + 400 + 50 + 7
1457
-
Sistem Bilangan Heksadesimal
Sistem ini adalah sistem menghitung bilangan yang berbasis 16, yakni 1,2,3,4,5,6,7,8,9,A,B,C,D,E & F. SIstem ini identik juga dengan sistem bilangan oktal sehingga bisa digunakan sebagai alternatif untuk menyederhanakan bilangan biner. Contohnya, 16 = 24, maka 1 digit bilangan heksadesimal mewakili 4 digit bilangan biner.
Dalam sistem heksadesimal, bilangan ditulis atau direpresentasikan dengan basis 16. Pada sistem heksadesimal, bilangan direpresentasikan terlebih dahulu seperti pada sistem desimal, yaitu dari 0 sampai 9. Kemudian bilangan tersebut direpresentasikan dengan menggunakan abjad dari A sampai F.
Tabel di bawah ini menunjukkan representasi angka dalam sistem bilangan heksadesimal :
| Hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
-
Sistem Bilangan Oktal
Berikutnya ada sistem bilangan octal, yaitu sistem yang memakai bilangan oktal, atau suatu cara menghitung yang memakai delapan simbol angka. Disebut juga dengan sistem bilangan berbasis 8, yang dimulai dari 0,1,2,3,4,5,6 dan 7.
Sistem ini umumnya dipakai untuk lebih menyederhanakan sistem kode biner. Umumnya bilangan oktal ini digunakan dalam aplikasi komputer. Berikut contoh penggunaan bilangan oktal pada konversi sistem bilangan.
Rubahlah bilangan oktal 2158 menjadi bentuk desimal :
2158 = 2 × 82 + 1 × 81 + 5 × 80
= 2 × 64 + 1 × 8 + 5 × 1
= 128 + 8 + 5
= 14110
-
Sistem Bilangan Real
Ada pula bilangan yang disebut sistem bilangan real, yaitu bilangan yang dapat dipakai dalam operasi bilangan sebagaimana yang dilakukan seperti biasa. Bilangan real disimbolkan dengan R. Bilangan real ini banyak digunakan untuk operasi perhitungan yang digunakan dalam kehidupan sehari-hari.
Sistem ini dibagi lagi menjadi 2, yaitu bilangan rasional dan bilangan irasional. Bilangan rasional merupakan sistem bilangan real yang bisa dinyatakan menjadi bentuk pecahan, dimana masing-masing bilangan adalah bilangan bulat dan bilangan penyebut tidak sama dengan 0.
Sementara bilangan irasional adalah numeric system yang tidak bisa dinyatakan ke dalam bentuk pecahan namun bisa dinyatakan dalam bentuk desimal. Contoh yang paling sering digunakan adalah phi = 3,14.
Sifat-Sifat Bilangan Real :
Bilangan real memiliki sifat khusus. Sifat sistem bilangan adalah sifat yang hanya dimiliki oleh bilangan real. Ada sifat tertutup, yaitu operasi penjumlahan dan perkalian antara bilangan real yang juga menghasilkan bilangan real. Selain itu, ada beberapa sifat lain yang hanya dimiliki oleh bilangan real.
a. Mempunyai Invers
Bilangan real memiliki sifat mempunyai invers. Artinya, setiap bilangan nyata memiliki invers real terhadap operasi perkalian dan penjumlahan. Artinya, apabila suatu bilangan nyata dikalikan atau dijumlahkan dengan inversnya, maka akan menghasilkan unsur identitas bilangan tersebut.
b. Bersifat Distributif
Sifat distributive pada sistem bilangan real artinya penyebaran dua operasi hitung berbeda. Salah satunya berfungsi untuk operasi hitung penyebaran sedangkan operasi lain dipakai untuk menyebarkan bilangan.
c. Tidak dapat Dibagi dengan Nol
Bilangan real memiliki sifat tidak ada pembagi nol. Jika bilangan real dibagi dengan nol, mak hasilnya adalah tidak terdefinisi.
Konversi Sistem Bilangan

Pada materi tentang sistem bilangan, terdapat pembahasan tentang konversi bilangan. Sebagaimana yang diketahui, sistem bilangan ada berbagai macam jenisnya.
Masing-masing jenis sistem bilangan itu kemudian masih bisa diubah menjadi sistem bilangan lain dengan cara konversi. Berikut ini akan dijelaskan secara singkat dan jelas tentang konversi dari bilangan desimal ke biner.
Dalam pembahasan sebelumnya, terdapat pembahasan yang membahas tentang basis bilangan. Setiap number system menggunakan suatu basis atau bilangan dasar tertentu.
Berkaitan dengan basis tersebut, bilangan dapat dikonversikan yang kemudian disebut dengan konversi sistem bilangan, yaitu proses satu sistem bilangan berbasis tertentu kemudian dikonversikan (diubah) menjadi bilangan berbasis lain.
Secara garis besar, yang dimaksud dengan konversi pada sistem bilangan ini adalah sebuah proses dimana suatu sistem bilangan dengan basis tertentu kemudian diubah menjadi sistem bilangan berbasis lain.
Misalnya pada contoh konversi bilangan desimal menjadi biner. Konversi ini dilakukan untuk mengubah sistem bilangan dengan basis 10 menjadi sistem bilangan biner dengan basis 2. Cara konversinya pun berbeda-beda.
Ada beberapa konversi yang bisa dilakukan, seperti konversi dari bilangan desimal ke biner atau sebaliknya, desimal ke oktal, desimal ke heksadesimal dan lain sebagainya. Cara konversi masing-masing bilangan pun berbeda dan memiliki aturan sendiri.
Sistem bilangan adalah salah satu materi dasar yang harus dipelajari dalam ilmu matematika karena bisa digunakan untuk banyak hal. Contoh sederhana mengenai konversi sistem bilangan bisa anda lihat pada ulasan dibawah ini :
a. Rubahlah bentuk angka 349 kedalam bentuk biner, desimal, oktal, dan hexadesimal !
Jawaban :
- Bilangan 349 dalam sistem bilangan desimal adalah 349.
- Bilangan 349 dalam sistem bilangan oktal adalah 535.
- Angka 349 dalam sistem bilangan biner adalah 101011101
- Angka 349 dalam sistem bilangan heksadesimal adalah 15D
Konversi Bilangan Desimal ke Bilangan Biner
Konversi dari bilangan desimal menjadi bilangan biner adalah dengan cara membagi bilangan desimal dengan 2 kemudian menyimpan sisa hasil pembagian per pembagian hingga hasil pembagiannya <2. Hasil konversinya merupakan urutan sisa pembagian dari paling akhir hingga yang paling awal.
Secara sederhana, konversi bilangan desimal ke biner ini dilakukan dengan membaginya dengan angka 2. Apabila dalam pembagian tersebut tidak ada sisa maka hasilnya sama dengan bernilai 0. Namun apabila bersisa, diterjemahkan dengan nilai 1.
Cara ini hanya berlaku untuk konversi dari bilangan desimal ke bilangan biner. Sedangkan untuk konversi bilangan biner ke desimal dilakukan dengan mengalikan bilangan biner yang akan dikonversikan dengan 2 lalu dipangkatkan dengan bilangan desimal mulai dari kanan.
Langkah-Langkah Konversi Bilangan Desimal ke Biner :
Agar lebih memudahkan proses konversi perhatikan langkah-langkah berikut.
- Tuliskan Soal Bilangan Desimal yang Akan Dikonversi
Tulis bilangan desimal yang akan dibagi di dalam pembagian susun. Tulis basis sistem yang dituju (bilangan biner adalah 2) sebagai pembagianya yang diletakkan di luar kurva lambang pembagian.
- Lakukan Pembagian
Jika sudah, lakukan pembagian bilangan desimal dengan 2. Tulis hasil baginya di bawah lambang bagi panjang. Jangan lupa juga tuliskan sisa pembagian, baik itu sisa 0 atau sisa 1 di sebelah kanan sejajar dengan bilangan desimal yang dibagi.
Untuk mempermudah, apabila bilangan yang dibagi adalah bilangan genap, maka sisanya pasti 0. Sementara jika bilangan yang dibagi adalah bilangan ganjil, maka sisanya pasti 1.
- Teruskan Pembagian Sampai Mencapai Nol
Lanjutkan operasi pembagian ini sampai bilangan desimal utama yang dibagi sudah mencapai 0. Jika sudah mencapai nol, selanjutnya bilangan biner sudah bisa disusun.
- Menyusun Bilangan Biner Baru
Terakhir tinggal menyusun bilangan biner baru hasil pembagian tersebut. Dimulai dari menyusun angka sisa paling bawah kemudian dibaca atau disusun secara berurutan dari bawah ke atas. Maka kemudian Anda akan mendapatkan bilangan biner baru hasil konversi dari bilangan desimal.
Konversi Bilangan Desimal ke Hexadesimal
Selain dikonversikan menjadi bilangan biner, bilangan desimal juga bisa dikonversikan menjadi bilangan heksadesimal. Karena bilangan heksadesimal adalah bilangan berbasis 16, maka konversi bilangan desimal ke hexadesimal dilakukan dengan cara membagi bilangan desimal dengan 16 lalu menyimpan sisa hasil baginya terus sampai hasil baginya < 16.
Apabila sisa hasil bagi di atas 9, maka angka sisa hasil bagi diubah menjadi huruf. Apabila sisa hasil 10, maka nilainya menjadi A, 11 menjadi nilai B hingga 15 menjadi nilai F.
Konversi Bilangan Oktal Ke Biner
Bilangan oktal memiliki angka berjumlah 8, tetapi bilangan biner adalah dari basis 2. Oleh karena itu, untuk mengubah bilangan oktal menjadi bilangan biner, basis dari bilangan tersebut harus diubah. Ikuti langkah-langkah yang diberikan di bawah ini:
- Langkah 1: Tulis setiap digit bilangan oktal secara terpisah.
- Langkah 2: Ubah setiap digit menjadi kelompok yang setara dengan tiga digit biner.
- Langkah 3: Gabungkan grup-grup ini untuk membentuk bilangan biner utuh.
Konversi Bilangan Oktal Ke Desimal
Bilangan Oktal diwakili dengan angka 0-7 dan dengan basis 8. Konversi sistem bilangan berarti konversi dari satu basis ke basis lainnya. Berikut ini adalah konversi Sistem Bilangan Oktal ke Sistem Bilangan Desimal.
Bilangan oktal diwakili dalam basis 8, tetapi bilangan desimal adalah basis 10. Oleh karena itu, untuk mengubah bilangan oktal menjadi bilangan desimal, basis dari bilangan tersebut harus diubah. Ikuti langkah-langkah yang diberikan di bawah ini:
- Langkah 1: Kalikan setiap digit bilangan Oktal dengan nilai tempat digit tersebut, mulai dari kanan ke kiri yaitu dari LSB ke MSB.
- Langkah 2: Tambahkan hasil perkalian ini dan angka desimal akan terbentuk.
Konversi Bilangan Oktal ke Hexadesimal
Bilangan oktal diwakili dalam basis 8, tetapi bilangan heksadesimal adalah basis 16. Oleh karena itu, untuk mengubah bilangan oktal menjadi bilangan heksadesimal, basis bilangan tersebut harus diubah. Ikuti langkah-langkah yang diberikan di bawah ini:
- Langkah 1: Kita perlu mengonversi bilangan Oktal ke Biner terlebih dahulu. Untuk itu, ikuti langkah-langkah yang diberikan dalam konversi di atas.
- Langkah 2: Sekarang untuk mengubah bilangan biner ke bilangan Hex, bagilah digit biner menjadi kelompok empat digit mulai dari kanan ke kiri yaitu dari LSB ke MSB.
- Langkah 3: Tambahkan nol sebelum MSB untuk menjadikannya kelompok empat digit yang tepat (jika diperlukan)
- Langkah 4: Sekarang ubah grup ini menjadi nilai desimal yang relevan.
- Langkah 5: Untuk nilai dari 10-15, ubah menjadi simbol Hex yaitu dari A-F
Konversi Bilangan Oktal Ke Biner
Bilangan oktal diwakili dalam basis 8, tetapi bilangan biner adalah dari basis 2. Oleh karena itu, untuk mengubah bilangan oktal menjadi bilangan biner, basis dari bilangan tersebut harus diubah. Ikuti langkah-langkah yang diberikan di bawah ini:
- Langkah 1: Tulis setiap digit bilangan oktal secara terpisah.
- Langkah 2: Ubah setiap digit menjadi kelompok yang setara dengan tiga digit biner.
- Langkah 3: Gabungkan grup-grup ini untuk membentuk bilangan biner utuh.
Konversi Heksadesimal ke Desimal:
Bilangan heksadesimal diwakili dalam basis 16 tetapi bilangan desimal adalah basis 10. Oleh karena itu, untuk mengubah bilangan heksadesimal menjadi bilangan desimal, basis bilangan tersebut harus diubah. Ikuti langkah-langkah yang diberikan di bawah ini:
- Langkah 1: Tulis nilai desimal dari simbol yang digunakan dalam bilangan Hex yaitu dari A-F
- Langkah 2: Kalikan setiap digit angka Hex dengan nilai tempatnya. mulai dari kanan ke kiri yaitu LSB ke MSB.
- Langkah 3: Tambahkan hasil perkalian dan jumlah akhir akan menjadi angka desimal.
Konversi Heksadesimal ke Biner:
Bilangan heksadesimal direpresentasikan dalam basis 16, tetapi bilangan biner adalah dari basis 2. Oleh karena itu, untuk mengubah bilangan heksadesimal menjadi bilangan biner, basis dari bilangan tersebut harus diubah. Ikuti langkah-langkah yang diberikan di bawah ini:
- Langkah 1: Ubah simbol Hex menjadi nilai desimal yang setara.
- Langkah 2: Tulis setiap digit angka Heksadesimal secara terpisah.
- Langkah 3: Ubah setiap digit menjadi kelompok yang setara dengan empat digit biner.
- Langkah 4: Gabungkan grup-grup ini untuk membentuk bilangan biner utuh.
Konversi Heksadesimal ke Oktal:
Bilangan heksadesimal diwakili dalam basis 16, tetapi bilangan oktal adalah basis 8. Oleh karena itu, untuk mengubah bilangan heksadesimal menjadi bilangan oktal, basis bilangan tersebut harus diubah. Ikuti langkah-langkah yang diberikan di bawah ini:
- Langkah 1: Kita perlu mengonversi bilangan Heksadesimal ke Biner terlebih dahulu. Untuk itu, ikuti langkah-langkah yang diberikan dalam konversi di atas.
- Langkah 2: Sekarang untuk mengubah bilangan biner ke bilangan Oktal, bagilah digit biner menjadi kelompok tiga digit mulai dari kanan ke kiri yaitu dari LSB ke MSB.
- Langkah 3: Tambahkan nol sebelum MSB untuk menjadikannya kelompok tiga digit yang tepat (jika diperlukan)
- Langkah 4: Sekarang ubah grup ini menjadi nilai desimal yang relevan.
Contoh Soal Sistem Bilangan
Untuk lebih memudahkan, perhatikan contoh soal konversi bilangan dari desimal menjadi biner berikut ini.
- Konversikan bilangan 45 menjadi bilangan biner
Jawab:
4510 =
45 : 2 = 22 (sisa 1 )
22 : 2 = 11 (sisa 0)
11 : 2 = 5 (sisa 1)
5 : 2 = 2 (sisa 1)
2 : 2 = 1 (sisa 0)
Jadi hasil konversinya adalah 1011012 (penulisan dilakukan dari bawah)
- Tentukan hasil Konversi Bilangan 156 ke bilangan biner
Jawab:
156 : 2 = 78 (sisa 0)
78 : 2 = 39 (sisa 0)
39 : 2 = 19 (sisa 1)
19 : 2 = 9 (sisa 1)
9 : 2 = 4 (sisa 1)
4 : 2 = 2 (sisa 0)
2 : 2 = 1 (sisa 0)
Jadi, hasil konversi dari 15610 100111002
Kesimpulan Materi :
Sistem bilangan yang menggunakan radiks atau basis 2 disebut Biner. Kemudian untuk sistem bilangan yang menggunakan radiks atau basis 16 disebut Heksadesimal dan sistem bilangan yang menggunakan radiks atau basis 8 disebut Oktal. Sedangkan Sistem bilangan yang menggunakan radiks atau basis 10 disebut Desimal.
| Besaran Pokok | Besaran Turunan |
| Besaran Vektor | Rumus Kecepatan |
Untuk lebih mudah dalam memahami konsep konversi ini, Anda bisa membuatnya dalam bentuk tabel konversi bilangan. Cara apapun bisa digunakan untuk lebih memudahkan dalam memahami konsep konversi ini.
Nah, penjelasan tentang sistem bilangan di atas semoga bisa menjadi referensi untuk menggerakan berbagai contoh soal sistem bilangan. Terimakasih telah mengunjungi wikielektronika.com, semoga sukses selalu.