Memahami dengan benar apa yang dimaksud besaran vektor dan besaran skalar☑️Kolompok yang termasuk besaran vektor & Skalar Plus Contoh Soal☑️
Banyak yang salah kaprah tentang membedakan antara besaran dalam ilmu fisika yakni vektor dan skalar. Kedua besaran tersebut memang memiliki kemiripan yang signifikan namun pada dasarnya sangat berbeda.
Nah, bagi kamu yang masih bingung membedakan pengertian, jenis jenis dan juga contoh masing masing dari besaran skalar dan besaran vektor, berikut ulasan kompleks dan detail yang bisa teman teman simak.
Pengertian Besaran Vektor

Secara umum, arti besaran merupakan sesuatu yang hasilnya dapat dilihat dan dinyatakan dalam bentuk angka. Kemudian jika diklasifikasikan berdasarkan arah serta nilai besarannya, besaran ini terbagi menjadi dua golongan yakni vektor dan skalar.
Keduanya menjadi sumber informasi yang dibutuhkan pada suatu perhitungan. Lalu apa yang dimaksud dengan besaran vektor itu sendiri ?
Dalam ilmu Fisika, definisi besaran vektor adalah kelompok besaran yang memiliki nilai besar dan bekerja dalam arah tertentu. Contoh besaran vektor seperti gaya dengan satuan N (kg m/s²) , percepatan dengan satuan m/s², kecepatan dengan satuan m/s, tekanan dengan satuan Pa, berat, momentum, massa, impuls, dll.
Umumnya besaran vektor digambarkan dengan panah yang memiliki arah dan panjang yang sama dengan besaran. Meskipun besaran vektor ini memiliki arah dan besar.
Namun ia tidak memiliki posisi, sehingga selama nilai panjangnya tidak mengalami perubahan, vektor juga tidak mengalami perubahan nilai jika dipindahkan sejajar dengan dirinya sendiri.
Konsep Dasar Besaran Vektor :

- Mempunyai titik tangkap
Syarat yang paling utama untuk menghitung vektor yaitu titik tangkap gaya benda tersebut. Titik tangkap bisa disebut juga dengan titik nol, dimana sebagai titik sebelum adanya pergeseran dari benda tersebut.
- Adanya arah
Arah memiliki peran besar dalam perhitungan vektor. Arah tersebut ditentukan oleh arah gerak dan tidak hanya berlaku untuk gerak lurus namun juga arah melengkung. Sebagai contoh gerak dari atas ke bawah saat melemparkan peluru atau bola.
- Nilai yang dapat ditetapkan
Besarnya nilai yang terdapat pada besaran vektor bisa diukur dengan menggunakan suatu alat. Umumnya nilai berbeda-beda tergantung jenis vektor yang diukur.
Misal menghitung suatu gaya, maka untuk dapat nilai vektor harus diukur dengan alat pengukur gaya atau tekanan. Apabila alat ukur menunjukkan hasil 40 Newton maka nilai vektor adalah 40 dengan satuan N atau newton.
- Perubahan Besaran Vektor
Besaran vektor ini bisa mengalami perubahan ketika berada dalam tiga kondisi. Kondisi yang pertama terjadi jika besarnya berubah, kondisi kedua terjadi jika arah mengalami perubahan, kondisi ketiga yakni ketika besar dan arah (keduanya) mengalami perubahan.
Contoh Pernyataan Besaran Vektor dalam Kehidupan Sehari hari :
Contoh besaran vektor dan skalar dalam kehidupan sehari hari bisa kita lihat pada saat seseorang mendorong mobil yang mogok. Mobil yang didorong menggunakan sebuah Gaya (F) yang menimbulkan perpindahan dan percepatan (a) mobil. Berikut contoh contoh lainnya :
- Arsya berpindah tempat duduk dari timur ke arah barat 2 bangku.
- Mobil yang mogok itu didorong menggunakan gaya 10 N kearah kiri.
- Kecepatan pesawat Lion Air dari arah Jakarta mencapai 100 m/s menuju ke selatan.
- Percepatan kedua motor itu sama persis 5 m/s menuju kearah barat
Kelompok Besaran Vektor
Seperti besaran pada umumnya dalam fisika, kelompok besaran vektor dan besaran skalar mempunyai satuan yang dapat menyatakan bahwa itu adalah besaran tersebut. Keduanya memiliki satuan yang berbeda-beda dilihat dari jenis, simbol dan ketetapan satuan Internasional.
Besaran vektor dan satuannya biasanya ditulis atau digambarkan dalam bentuk arah panah yang lurus. Arah tersebut merupakan gambaran yang mewakili petunjuk besar dan arah vektor. Dengan kata lain 1 dimensi vektor mewakili 1 komponen vektor dan seterusnya.
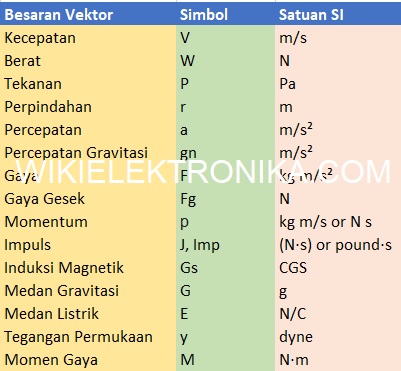
Kelompok besaran vektor mempunyai satuan dengan simbol yang berbeda-beda. Berikut ini yang termasuk besaran vektor disertai simbol dan satuan internasional :
| Besaran Vektor | Simbol | Satuan SI |
| Kecepatan | V | m/s |
| Berat | W | N |
| Tekanan | P | Pa |
| Perpindahan | r | m |
| Percepatan | a | m/s² |
| Percepatan Gravitasi | gn | m/s² |
| Gaya | F | kg m/s² |
| Gaya Gesek | Fg | N |
| Momentum | p | kg m/s or N s |
| Impuls | J, Imp | (N⋅s) or pound⋅s |
| Induksi Magnetik | Gs | CGS |
| Medan Gravitasi | G | g |
| Medan Listrik | E | N/C |
| Tegangan Permukaan | y | dyne |
| Momen Gaya | M | N⋅m |
| Torsi | N | HP or PS |
Rumus Besaran Vektor
Untuk menemukan hasil dari perpindahan besaran vektor harus dihitung dengan aturan tertentu. Berikut ini adalah rumus besaran vektor atau metode yang digunakan untuk menghitung besaran vektor.
- Menghitung Besar dan Arah Resultan Vektor

Perhatikan gambar diatas, Untuk menetukan besar dan arah vektor resultan seperti yang ditunjukkan pada grafik garis tersebut, digunakan rumus :

- Menghitung Perkalian Besaran Vektor
Rumus perkalian vektor memiliki dua jenis, yang pertama yaitu perkalian titik (dot product) dan yang kedua adalah perkalian silang (cross product), Berikut ulasannya :
a. Perkalian Titik
Perkalian titik dari dua vektor A dan B dilambangkan dengan A • B. Perkalian titik dari dua vektor A dan B yang mengapit sudut θ dapat didefinisikan sebagai berikut :
A • B = AB cos θ
Sifat-sifat perkalian titik di antara sesama vektor satuan sebagai berikut :
i • i = j • j = k • k = (1)(1).cos 0° = 1
i • j = i • k = j • k = (1)(1).cos 90° = 0
Pada perkalian titik antara dua vektor bersifat komutatif, yaitu :
A • B = B • A
Perkalian titik dari dua buah besaran vektor inilah yang akan menghasilkan besaran skalar.
b. Perkalian Silang
Perkalian silang antara dua vektor A dan B dilambangkan dengan A x B. Perkalian silang antara dua vektor A dan B yang mengapit sudut θ digambarkan dengan persamaan berikut ini :
C = A x B
C = AB sin θ
Perkalian silang dari dua vektor A dan B yang mengapit sudut θ adalah suatu besaran vektor yang arahnya tegak lurus terhadap kedua vektor dan besarnya sama dengan AB sin θ .
Sifat-sifat perkalian silang di antara sesama vektor satuan bisa anda lihat dibawah ini :
i x i = j x j = k x k = 0
Dengan :
| i x j = k | j x i = -k |
| j x k = i | k x j = -i |
| k x i = j | i x k = -j |
Perkalian silang antara dua vektor bersifat anti komutatif, yaitu A x B = -B x A
- Menghitung Besaran Vektor dengan Metode Jajar Genjang

Sesuai dengan namanya, maka untuk menghitung nilai dari besaran vektor ini bisa ditemukan jika menggambar jajar genjang terlebih dahulu. Kemudian tentukan besaran nilai yang ada dan hitung besaran nilai gabungan dari dua vektor yang ada.
- Menghitung Besaran Vektor dengan Metode Analisis

Untuk metode satu ini harus dijabarkan terlebih dahulu. Sumbu yang ditempati disimbolkan dalam bentuk X dan Y. Kemudian diuraikan sesuai adalah sumbu masing-masing. Setelah nilai tiap sumbu berhasil dihitung maka, hasil kedua sumbu yang searah dijumlahkan. Dan terakhir resultan kedua vektor dari dua sumbu yang telah dijumlahkan tersebut.
- Metode Besaran Vektor dengan Gambar Vektor atau Grafis (Polygon)

Dibanding yang lainnya, metode yang terakhir ini cukup komplek. Pertama gambar vektor terlebih dahulu dengan perhitungan cermat serta pengukuran yang pas. Bagian tersebut perlu ketelitian agar hasilnya sesuai dengan gambar.
Perhitungan dengan metode ini memiliki kelemahan yakni cukup sulit untuk mendapatkan hasil sesuai dengan keadaan yang sebenarnya. Sedikit saja kesalahan maka hasil akan bergeser dan berbeda.
Pengertian Besaran Skalar

Definisi besaran skalar adalah kuantitas yang hanya memiliki nilai numerik magnitudo (besaran) saja tanpa memiliki Arah. Contoh besaran skalar seperti panjang dengan satuan meter, waktu dengan satuan second, suhu dengan satuan Kelvin, usaha dengan satuan Joule, arus listrik, intensitas cahaya, jumlah zat, dll.
Dalam cabang ilmu Fisika juga disebutkan bahwa besaran skalar adalah besaran yang tidak mengalami perubahan dalam rotasi koordinat (atau transformasi Lorentz, sebagai relativitas). Berikut ragam contoh besaran skalar lengkap dengan simbol dan satuan internasional (SI) nya :
Contoh Besaran Skalar & Satuannya
| Besaran Skalar | Simbol | Satuan SI |
| Waktu | T | Second (s) |
| Jarak | s atau d | meter (m) |
| Massa Jenis | ρ (rho) | g/cm3 |
| Perpindahan | Δx atau Δr | meter |
| Panjang | L | meter (m) |
| Suhu | θ (theta) | kelvin (k) |
| Volume | V | meter kubik (m3) |
| Kelajuan | v | m/s |
| Daya | P | Watt |
| Usaha | W | joule (J) |
| Muatan Listrik | Q | Coloumb (C) |
| Potensial Listrik | V | Volt (v) |
| Jumlah Zat | N | mol |
| Kerapatan Arus | J | A/mm2 |
| Energi Kinetik | KE, Ek, or T | joule (J) |
| Energi Potensial | PE, U, or V | joule (J) |
Contoh Besaran Skalar dalam Kehidupan Sehari hari :
- Laju kereta api itu menembus angka 20 m/s
- Panjang gambar penggaris kartun itu adalah 10 meter
- Daya listrik rumah minimalis umumnya menggunakan kapasitas 1200 watt
- Massa beras dalam satu karung tersebut adalah 25 kg
- Jarak dari kampus menuju kos kosan arsya adalah 13 Km
- Arus listrik pada UPS komputer tersebut berkapasitas 500 Ampere
- Temperatur suhu pada air sungai di pedalaman tersebut mencapai 8′ Kelvin saat diukur dengan termometer digital.
Soal Besaran Vektor dan Besaran Skalar

Sesuai dengan penjelasan sebelumnya, baik vektor dan skalar memiliki kasus yang berbeda. Sebagai kasus contoh besaran skalar
1. Seekor semut sedang berjalan dan melintasi jalan dari titik A ke B. Dalam menempuh perjalanan semut melintasi jarak sebesar 30cm dan mengalami perpindahan menuju titik B sebanyak 15cm.
Pembahasan :
Maka jika dijabarkan, jarak yang ditempuh semut sebesar 30cm tersebut merupakan contoh besaran skalar yang cukup dituliskan nilainya saja. Sedangkan perpindahan menuju titik B merupakan contoh besaran vektor dimana dijabarkan baik perpindahan suatu titik dan jaraknya.
2. Satelit geostasioner mengorbit di atas bumi. Bergerak dengan kecepatan konstan tetapi kecepatannya terus berubah (karena arahnya selalu berubah).
Pembahasan :
# Selisih dua besaran vektor = vektor akhir – vektor awal
# Selisih dua besaran skalar = nilai besar – nilai kecil
3. Diketahui sebuah garis vektor memiliki persamaan nilai dibawah ini :
Ā = 3i – 2j + k
B = i + j + 4k
Tentukan: Ā x B !
Pembahasan :

Jadi Nilai dari perkalian Ā x B adalah -9i – 11j + 5k
4. Sebuah garis vektor membentuk persamaan dibawah ini :
Ā = 3i – 2j + k
B = i + j + 4k
Tentukan nilai dari Ā •B !
Pembahasan :
Ā •B = (3.1)+ (-2.1) + (1.4) = 3 – 2 + 4 = 5
Jadi nilai dari perkalian Ā •B adalah 5
Kesimpulan Materi :
a. Perbedaan besaran vektor dan skalar terletak pada “Arah” saja. Vektor adalah besaran yang sepenuhnya dijelaskan baik oleh besaran maupun arah sedangkan Skalar adalah besaran yang sepenuhnya dijelaskan oleh nilai numerik saja (‘tidak memiliki arah’).
b. Contoh besaran vektor seperti kecepatan, tekanan dan perpindahan. Sedangkan contoh besaran skalar seperti Jarak, Waktu dan Suhu.
c. Sebuah Vektor diwakili oleh gambar panah. Panah menunjukkan arah vektor, sedangkan panjang panah menunjukkan besarnya
d. Vektor dapat digabungkan dengan menambahkan atau menguranginya satu sama lain menggunakan metode jajaran genjang, maupun segitiga.
e. Ketika dua atau lebih vektor ditambahkan bersama-sama (atau satu dikurangkan dari yang lain), sebuah vektor tunggal terbentuk dan dikenal sebagai vektor resultan.
f. Dua vektor dapat diwakili oleh satu vektor resultan yang memiliki efek yang sama
g. Vektor resultan tunggal dapat diselesaikan dan diwakili oleh dua vektor, yang dalam kombinasinya memiliki efek yang sama dengan vektor aslinya
h. Ketika vektor resultan tunggal dipecah menjadi bagian-bagiannya, bagian-bagian itu disebut komponen.
| Besaran Pokok | Besaran Turunan |
| Pengertian Histogram | Gerbang Logika Dasar |
Demikian ulasan mengenai besaran vektor dan besaran skalar dalam cabang ilmu fisika yang bisa wikielektronika.com ulas. Untuk menghitung besaran vektor perhatikan syarat hitung terlebih dahulu lalu gunakan metode yang sesuai seperti penjelasan di atas.
Terimakasih. Sangat bermanfaat.